
- or -
Avoiding the Low Power Landmine
- or -

- or -
The exit pupil of any telescope/eyepiece combination is the image of the objective lens (or mirror) formed by the eyepiece, which is seen directly behind the eye lens. It can also be thought of as the beam of light that emerges from the eyepiece. The diameter of this beam can be measured directly using a good scale or ruler and a magnifier. Or it can be computed by dividing the objective lens diameter by the magnification of the system. For instance, for a 7x35 binocular, the diameter of the objective lens (35 millimeters), divided by the magnification (7x) equals an exit pupil of 5 millimeters.
For decades, the 7x50 binocular has been considered to be the standard "night glass", or the binocular used for delivering maximum image brightness in night-time conditions for maritime or military use. This is because the fifty millimeter objectives collect a lot of light, and the low, 7 power magnification delivers the widest field of view, while keeping the exit pupil within a maximum value of 7 millimeters, which is generally considered the maximum diameter that the pupil of the average human eye will dilate to in darkness. That is, the average eye of a young person of average military age!
This number decreases with age however. An eighty-year-old person's pupils may only dilate to 2 or 3 millimeters. A lot of us are somewhere between those two figures and all of us will be eventually! I am in my forties and have measured my dilated pupil to be 5.5 to 5.8 millimeters in the middle of the night at a dark-sky site.
The important point here is that any portion of an optical system's exit pupil that exceeds the eye's pupillary diameter is not collected by the eye and is lost or wasted light.
For example, imagine looking through a 10x70 binocular in dark conditions. The binocular delivers a 7mm exit pupil (70 divided by 10 = 7). We'll assume your eye is dilated to 7 millimeters, and is accepting the full amount of light collected by the 70mm objective lenses. Now imagine using the same binocular in twilight conditions when the pupil of your eye is dilated to only 5 millimeters. Two millimeters of the binocular's exit pupil is wasted light because your eye can only accept 5 millimeters. So in effect, the 10x70's under these conditions are only delivering into your eye the light that a pair of 10x50's would.
In bright daylight conditions your eye is only dilated to perhaps 2 millimeters so those 10x70's are only delivering to your eye the light that a pair of compact 10x20's would! There is no point to dragging those big 70mm binoculars around with you on a sunny day at the beach, is there?
This brings up two interesting questions and the point of this article:
Let's imagine that I just got a shiny new 8 inch f/4 Newtonian telescope for wide angle deep sky observing and a big beautiful 55mm low power eyepiece to go with it. I say to myself, "Hmmm, eight inches times f/4, is thirty-two inches of focal length; "
"times 25.4 to convert to millimeters equals about 813 millimeters of focal length;"
32 x 25.4 = 812.8 millimeters focal length
"813 divided by my 55mm eyepiece is, uhh, about 15 power."
812.8 / 55 = 14.78 power
"Wow!", I say. "The 50 degree apparent field of this eyepiece, divided by 15 power, gives me almost a three and a half degree field of view!" This is true,
8 x 25.4 = 203
If I divide that by 14.78 power,
203 / 14.78 = 13.73mm exit pupil
we find that my big beautiful eyepiece is delivering a
whopping 13.7 millimeter exit pupil to the little 7 millimeter pupil of my eye!
If I find the area of that 13.73 mm exit pupil
(13.73 / 2)^2 x pi = 148.06 square millimeters
and the area of my eye's 7mm pupil,
(7 / 2)^2 x pi = 38.5 square millimeters
then divide the exit pupil's area by my eye's area I get a ratio:
148.06 / 38.5 = 3.85 ratio
Now, if I find the light-collecting area of my 8 inch scope
(203 / 2)^2 x pi = 32365.5 square millimeters
and divide that by my ratio I get the area of my telescope's aperture that is actually able to send light into my eye.
32365.5 / 3.85 = 8406.6
Now I can divide that area by pi to get the radius squared,
8406.6 / pi = 2676
then find the square root to get the radius
sqrt 2676 = 51.729
and double that figure to get the equivalent diameter.
51.729 x 2 = 103.46
Now I can convert back to inches:
103.45 / 25.4 = 4.07 inches useful telescope diameter.
Now we simply divide our 8 inch telescope's diameter by this ratio to get the telescope's useable light-collecting area:
8 / 1.96 = 4.08 inches of useful telescope diameter.
In other words, with this eyepiece my 8 inch telescope seems to be delivering (to a young person's eye) only the amount of light collected by a 4 inch telescope!
But wait a minute! We're still not done! That eight inch telescope was provided with a large diagonal mirror to fully illuminate a large field, perhaps for photography. Let's say it has a 2.14 inch diagonal. The shadow that diagonal makes on the primary mirror is 3.6 square inches. With my eye's pupil (through that eyepiece) effectively stopping down my eight inch mirror to 3.2 inches (which is about 8 square inches of light collecting area), and the diagonal blocking 3.6 square inches of it, that leaves only 4.4 square inches of the telescope's light collecting area that reaches my eye.
That's only 60mm! No wonder the view looks brighter in my 70mm finderscope!
The finder has a wider field field of view too.
Let's work another example: How about a garden variety 10" f/4.5? Ten times f4.5 is 45, times 25.4 is 1143mm focal length; divided by our 55mm eyepiece, yields about 21 power. Our ten inch mirror has a 254mm objective diameter which, when divided by 21 power, yields a 12mm exit pupil! No good!
Surely that eyepiece would work well on say, a big 20" f/5? Work the numbers, and you'll find that you are still getting an 11 millimeter exit pupil! Assuming a 5 inch diagonal and a personal pupil of 5.5mm, with this eyepiece
Obviously, the 55mm eyepiece is not the right one for these fast f/ratio telescopes.
This was an extreme but realistic example using commonly available off-the-shelf components. I have seen people step on this landmine regularly. Let the buyer beware. However, there may be times that sacrificing some of our light like this is justified, for gaining a wider field of view.
As an example, say I have a dark-adapted pupillary diameter of six millimeters, and an f/5 telescope. Six times five equals thirty. If I use an eyepiece with a focal length any longer than 30 millimeters, I am effectively stopping down my telescope's light collecting area.
Now let's return to our brand new shiny 8 inch f/4 and determine what the actual rich field, low power eyepiece should be. Let's say our eye dilates to 6 millimeters under our blackest sky. Our f/4 telescope, times our 6mm eye, equals 24 millimeters. Our job now is to find a 24mm (or slightly less) eyepiece that works well on a fast f/4 system, with the widest apparent field of view!
| F | O | C | A | L | R | A | T | I | O | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.5 | 3.8 | 4 | 4.5 | 5 | 5.6 | 6 | 6.3 | 7 | 8 | 10 | 11 | 12 | 15 | ||
| 3.0 | 10 | 11 | 12 | 14 | 15 | 17 | 18 | 19 | 21 | 24 | 30 | 33 | 36 | 45 | |
| E | 3.5 | 12 | 13 | 14 | 16 | 18 | 20 | 21 | 22 | 25 | 28 | 35 | 38 | 42 | 53 |
| X | 4.0 | 14 | 15 | 16 | 18 | 20 | 22 | 24 | 25 | 28 | 32 | 40 | 44 | 48 | 60 |
| I | 4.5 | 16 | 17 | 18 | 20 | 23 | 25 | 27 | 28 | 32 | 36 | 45 | 49 | 54 | 68 |
| T | 5.0 | 18 | 19 | 20 | 23 | 25 | 28 | 30 | 32 | 35 | 40 | 50 | 55 | 60 | 75 |
| 5.5 | 19 | 21 | 22 | 25 | 28 | 31 | 33 | 35 | 38 | 44 | 55 | 61 | 66 | 83 | |
| P | 6.0 | 21 | 23 | 24 | 27 | 30 | 34 | 36 | 38 | 42 | 48 | 60 | 66 | 72 | 90 |
| U | 6.5 | 23 | 25 | 26 | 29 | 33 | 36 | 39 | 41 | 46 | 52 | 65 | 72 | 78 | 98 |
| P | 7.0 | 25 | 27 | 28 | 32 | 35 | 39 | 42 | 44 | 49 | 56 | 70 | 77 | 84 | 105 |
| I | 7.5 | 26 | 28 | 30 | 34 | 38 | 42 | 45 | 47 | 53 | 60 | 75 | 83 | 90 | 113 |
| L | 8.0 | 28 | 30 | 32 | 36 | 40 | 45 | 48 | 50 | 56 | 64 | 80 | 88 | 96 | 120 |
| 8.5 | 30 | 32 | 34 | 38 | 43 | 48 | 51 | 54 | 59 | 68 | 85 | 94 | 102 | 127 | |
| 9.0 | 32 | 34 | 36 | 41 | 45 | 50 | 54 | 57 | 63 | 72 | 90 | 99 | 108 | 135 |
To determine what your personal pupillary diameter is you need a method to measure it.
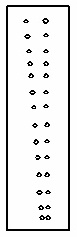
Take a piece of paper card stock (about 1 x 5 inches) and draw two slightly diverging lines on it. Then use a needle or safety pin to put several pairs of holes along the lines, about ½ inch apart. With care, most pairs will turn out to be of differing separations varying from about 8 or 9 millimeters, down to about 2 or 3 in roughly half-millimeter steps. Measure the separation of the holes, not from center to center, but from inner edge to inner edge. The use of a good ruler and a magnifier is required to measure them accurately. Label the pairs with their separation distances.
To use the thing, just hold it up to your eye and peer through the holes. Select the pair that appears as if the holes merge to the point that their inner edges just touch but don't overlap. Your pupillary diameter is then read from your pre-marked labels.
From a dark site the sky should provide just enough light to do the trick. If not, look through the device at a faintly illuminated object like a white car or the side of a building.
You now have a baseline for determining the lowest usable magnification for your telescope that won't waste aperture.
The exit pupil diameter is a very handy tool you can use to determine unknown factors of a telescope. Suppose you find a great deal on a well made military surplus telescope of some kind, but you don't know any of it's specifications. By focusing the thing at infinity (or something very far away), then measuring the objective lens diameter and the exit pupil size, simple division will give you the scope's magnification.
Let's say you were actually interested in getting the scope for the big beautiful Erfle eyepiece attached to it, but you don't know the eyepiece's focal length. By measuring the focal length of the instrument's objective lens (by guesstimating with a ruler prior to purchase) then dividing that figure by the magnification you found in the previous step, you will know the eyepiece's approximate focal length. It is a simple matter to do the inverse of this and find the focal length of an unknown objective (or mirror) by using an eyepiece of known focal length. Simple and handy.
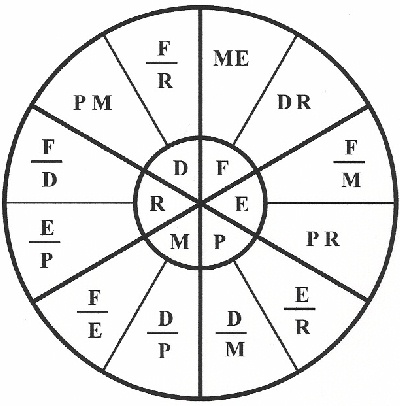
I designed this diagram to keep in my wallet as a handy telescope formula reference. Feel free to print one out for your own use. With these formulas you can determine unknown factors of a telescope/eyepiece combination by using factors that are known.
Enjoy!
I hope this little exercise served to enhance your enjoyment of the night sky.
- Jim Sapp
Autumn 1999 (Updated Spring 2003)